Stock Return and Fundamental Clustering & Portfolio Selection

Better portfolio management & optimization with machine learning / clustering
Author

Murat Koptur

Published

August 26, 2022

Introduction

Source: https://www.pexels.com/tr-tr/fotograf/belgenin-ustundeki-buyutec-6801648/

We have following features for BIST30 stocks:

  • Momentum 3-months, 6-months, 1-year

  • Volatility 1-year, 2-year, 3-year

  • Price-To-Book Ratio

  • Market Capitalization

  • Return On Equity

  • Earnings Growth

library(readr)
data <- read_csv("data.csv")
data <- as.data.frame(data)
row.names(data) <- data$stock
data

We need to standardize the features:

```{r}
library(scales)

cols <- 5:ncol(data)

data_scaled <- lapply(data[, cols], function(x) if(is.numeric(x)) rescale(x, to=c(0,1)) else x)
data_scaled <- as.data.frame(data_scaled)
data_scaled <- cbind(data[,1:4], data_scaled)
row.names(data_scaled) <- data_scaled$stock
data_scaled$stock <- NULL
data_scaled
```

Earnings Growth column has NA values, replace NA’s with zero:

data_scaled$earningsGrowth[is.na(data_scaled$earningsGrowth)] <- 0

We will use K-means method. Let’s calculate silhouette score for optimal cluster count:

library(factoextra)
library(cluster)

fviz_nbclust(data_scaled, kmeans, method = "silhouette", k.max = 10)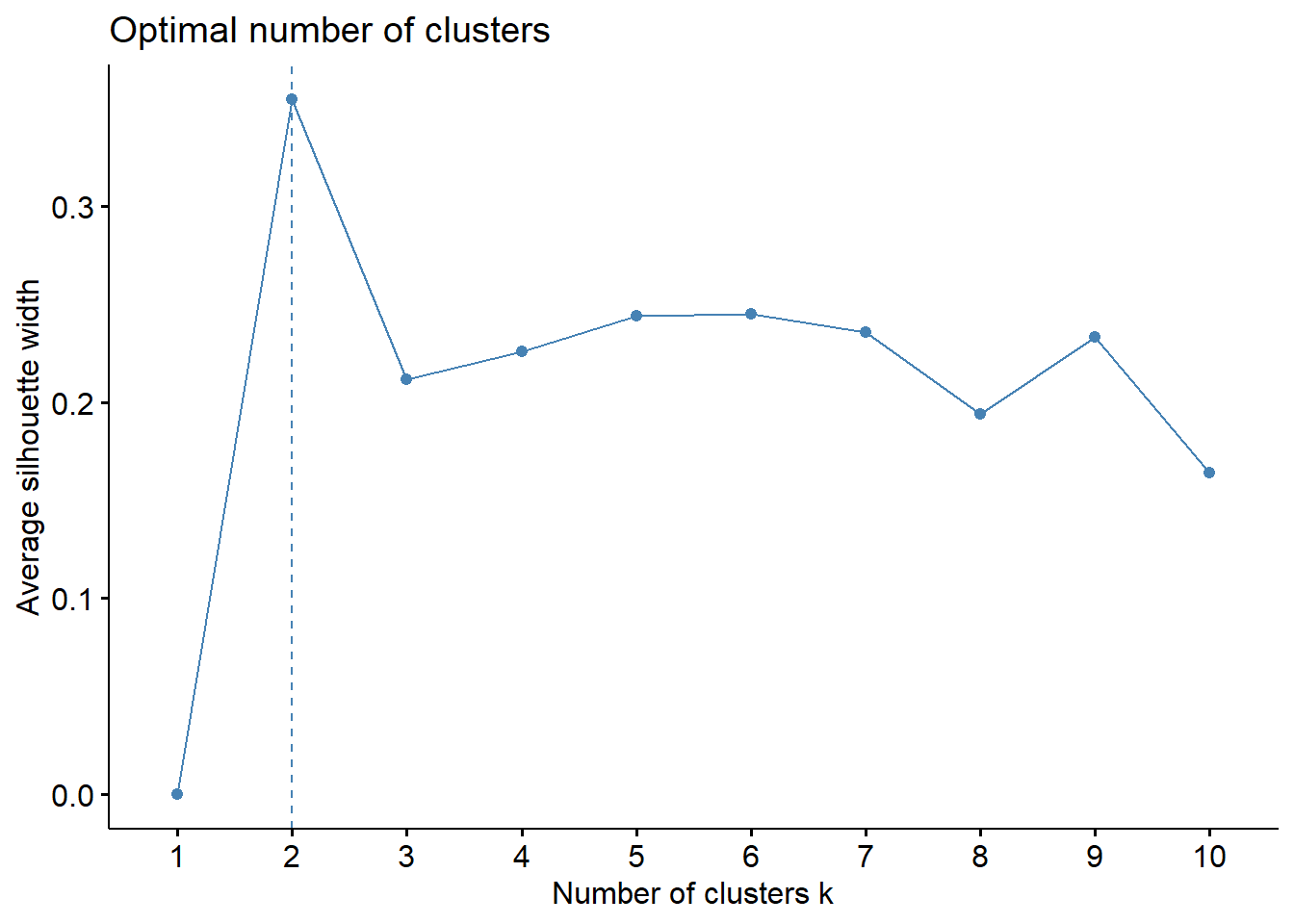

We have two different clusters, let’s fit model and see results:

model <- kmeans(data_scaled, 2)
fviz_cluster(object = model,
             data = data_scaled,
             ellipse.type = "norm",
             geom = "text",
             palette = "jco",
             main = "",
             ggtheme = theme_minimal())

Statistics:

model
K-means clustering with 2 clusters of sizes 24, 6

Cluster means:
   return1y  return2y  return3y momentum_3m momentum_6m momentum_1y
1 0.5021594 0.6856488 0.9261702   0.5014242   0.4282937   0.3035298
2 0.6812538 1.2212164 1.8785916   0.5867881   0.5896588   0.4708884
  volatility_1y volatility_2y volatility_3y priceToBook marketCap
1     0.1032558     0.0909333    0.07866424  0.03512632 0.3220344
2     0.4404008     0.4355551    0.39217887  0.34549470 0.6317486
  returnOnEquity earningsGrowth
1      0.3900359      0.1203581
2      0.5562222      0.2889656

Clustering vector:
TUPRS.IS VAKBN.IS KRDMD.IS DOHOL.IS AKBNK.IS TKFEN.IS FROTO.IS GARAN.IS 
       2        1        1        1        1        1        2        1 
KOZAA.IS HALKB.IS TCELL.IS KOZAL.IS VESTL.IS YKBNK.IS TTKOM.IS BIMAS.IS 
       1        1        1        1        1        1        1        1 
PETKM.IS ARCLK.IS EREGL.IS SAHOL.IS EKGYO.IS THYAO.IS PGSUS.IS ISCTR.IS 
       1        1        1        1        1        2        1        1 
KCHOL.IS ASELS.IS TAVHL.IS GUBRF.IS  SISE.IS  SASA.IS 
       1        1        1        2        2        2 

Within cluster sum of squares by cluster:
[1] 14.45341 10.20335
 (between_SS / total_SS =  26.7 %)

Available components:

[1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
[6] "betweenss"    "size"         "iter"         "ifault"      
sil <- silhouette(model$cluster, dist(data_scaled))
fviz_silhouette(sil, palette = "jco", ggtheme = theme_classic())
  cluster size ave.sil.width
1       1   24          0.45
2       2    6         -0.02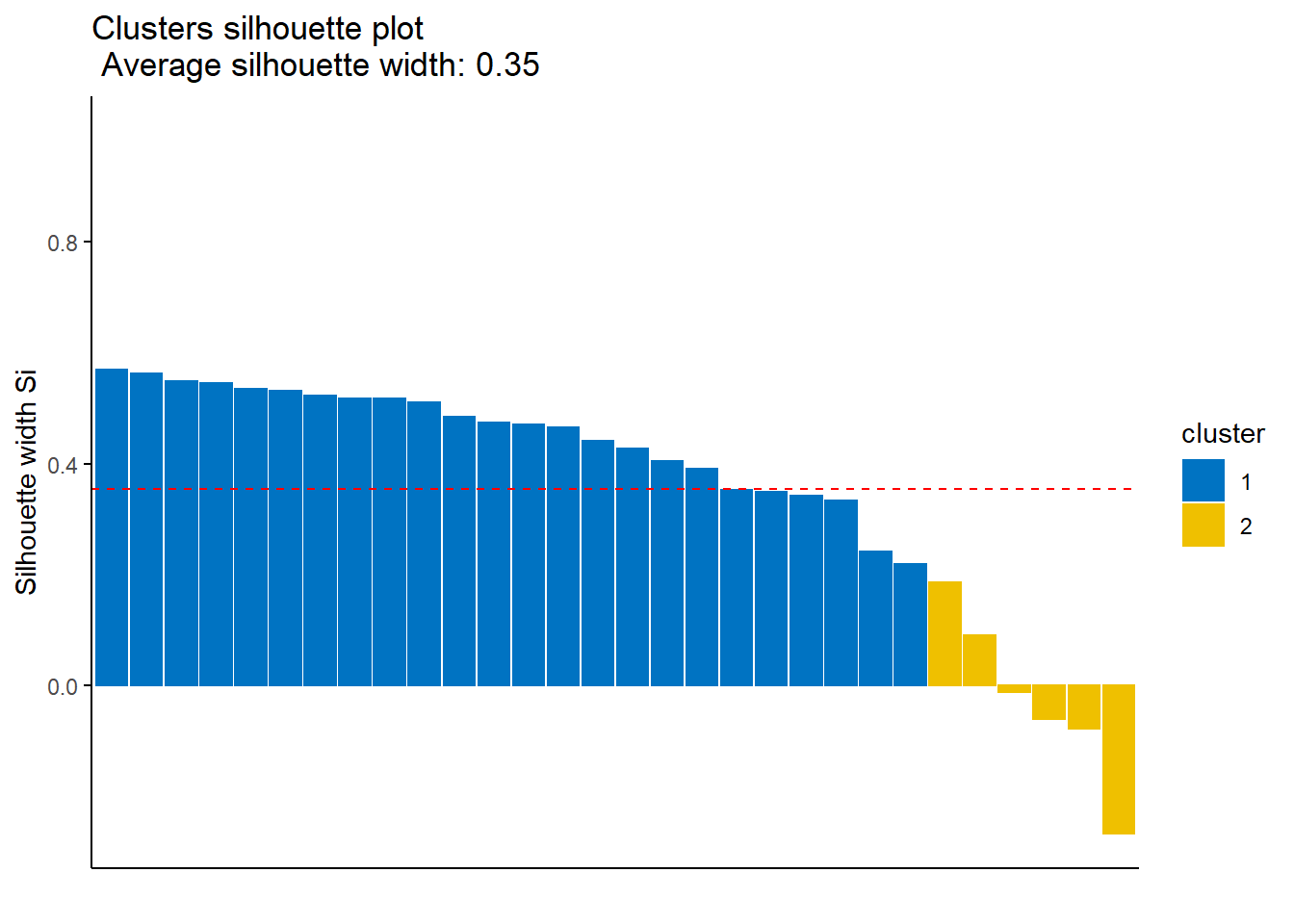

There are negative silhouette scores, it indicates that it may be in the wrong cluster.

Let’s look the mean return statistics of each cluster:

library(dplyr)

predicted_clusters <- data.frame(predicted_cluster=model$cluster, row.names=names(model$cluster))
data_clustered <- merge(data, predicted_clusters, by=0)

data_clustered %>%
  group_by(predicted_cluster) %>%
  summarise(
    mean_1_year_return = mean(return1y),
    std_1_year_return = sd(return1y),
    mean_2_year_return = mean(return2y),
    std_2_year_return = sd(return2y),
    mean_3_year_return = mean(return3y),
    std_3_year_return = sd(return3y),
    )

Full source code: https://github.com/mrtkp9993/MyDsProjects/tree/main/StockClustering

References

\(^1\) https://www.investopedia.com/terms/c/cluster_analysis.asp

\(^2\) https://www.investopedia.com/terms/f/factor-investing.asp

No matching items

Citation

BibTeX citation:
@online{koptur2022,
  author = {Koptur, Murat},
  title = {Stock {Return} and {Fundamental} {Clustering} \& {Portfolio}
    {Selection}},
  date = {2022-08-26},
  url = {https://www.muratkoptur.com/MyDsProjects/StockClustering/Analysis.html},
  langid = {en}
}
For attribution, please cite this work as:
Koptur, Murat. 2022. “Stock Return and Fundamental Clustering & Portfolio Selection.” August 26, 2022. https://www.muratkoptur.com/MyDsProjects/StockClustering/Analysis.html.